遠藤諭の東京カレー日記ii

引越し記念！ よりぬき東京カレー日記（8）

三等分家

　『角の三等分』（矢野健太郎・一松信著、筑摩文庫）の巻末に収録されている元数学セミナー編集長の亀井哲治郎氏の文章が面白かった。数学雑誌の編集部では「角の三等分の証明ができました」と読者が言ってきても「相手をするな」というのが先輩からのきついお達しだった。ところが、あるとき魔がさして１人の「三等分家」のお手紙に返事を書いてしまう。それから、延々と証明とその問題点の指摘のやりとりが何日も続き、相手のオジサンがあまりにしつこいので、最後は、電話が来たときに怒鳴りつけてしまったというお話。なんだか、可哀想なような、後悔の念にさいなまれたというような懺悔っぽい文章だった。

　パソコン雑誌の編集部にいた私としては、昔は、「こんな画期的なキーボードを開発しました」という発明家の方に何度かお付き合いしたことがある。それで、この『数学セミナー』の編集部のお話、ウンウン分かる分かると読ませてもらった（私もちょっと申し訳ない）。角の三等分と異なり全てではないのだが、そうして持ち込まれるキーボードというのは、正直かなりつらいことが多いのだ（数学の証明問題ほど白黒が付くわけじゃないので、ホホウナカナカみたいなこともごくまれにあるのだが）。

　ところが、亀井氏の文章には気になることが１つ書いてあった。最近は、小中学校で幾何の問題をあんまりやらなくなっているのだそうだ。どちらかというと、まともな計算問題よりも幾何学とか、論理的な証明問題のほうが好きだった私としては、これはたしかに気になる話。亀井氏は、そうしたことの結果、「角の三等分の証明が出来ました！」と数学雑誌の編集部に持ち込む人もいなくなるんではないかと。それは寂しいみたいなことを書かれているのだ。

　たしかに、画期的なキーボードの発明もさいきんトント聞かないような気もする。そのくらいポジティブに、「自分こそ画期的なアイデアを思いついた！」という人の母数がいないと、日本からはもう楽しい発明は出てこないかもしれない。

　ところで、このようなお話を書いていたら「エンドウさんだって角の三等分の話を書いてたでしょ」と言われた。「三等分家」というのは、英語では「Trisector」と言って解けないことが証明されている「任意の角の三等分の方法」を、「できたできた」と騒ぎたてる人のことをまさにそういうらしい。なんだか、オレも三等分家と思われているのもクヤシイので、こんなニュアンスの原稿だったのだよというのを、面倒なので全文引用しておくことにします（初出『月刊アスキー』1992年5月号、『近代プログラマの夕2』アスキー刊）。題名は「大工の源さんならデキルだよ」という文章だ。

任意の角を３等分する

　ギリシャの三大難問といえば、「任意の角を３等分する」、「立方体の２倍の体積の立方体を作る」、「円と等しい面積の正方形を描く」の３つの作図問題である。

　この３つの問題、ギリシャ時代というからには、実に、紀元前４世紀頃から2000年間にわたって解かれたことがないということになる。中学校の数学の時間などに、カーディガンなど妙に似合っちゃう数学の先生が、「任意の角を３等分する……」などと黒板にわけじり顔で書きはじめたりする。それで、クツワの三角定規と鉛筆装着型のコンパスであれこれやってみるのだが、そうは簡単には解けるはずがない。という経験のある方も少なくないだろう。

　とくに「任意の角を３等分する」という問題は、シンプルそのもので、手のひらに入るちっぽけな知恵の輪を思わせる風情があった。ところが、他の２つの問題とともに、久しく作図不可能とされてきたのである。それどころか、すでに解けないことが代数的に証明されているはずのものなのだという。解けそうで解けないところが、この問題の人気の秘密というか有名な理由である。2000年もの間、想像もできないほどの数の優れた頭脳のチャレンジを受け、ことごとく退けてきたわけなのだ。それが、

大工の源さんならデキるだよ

というのが今回のお話である。

　これには、直角定規を使う。原理は簡単、図１のとおりである。一見、何の変哲もなくパッと線を１本引いて（この線と角をなす１つの半直線が定規の幅であるところに注意！）、なにげなく定規を置いたら、アラ不思議、もう解けている。

　正確には定規とコンパスだけじゃなくて、直角定規を使うので、「幾何学的アプローチ」という観点からは、ちょっとズルかもしれないが、「あらヨっ」とかなんとか言って、とにかく大工さんにはできてしまう。このスピード感がいい。作図問題というよりも職人ワザというのにふさわしい超早ワザなところがいいでしょう。この感覚、実際に厚紙か何かで直角定規を作ってぜひ味わってみてほしい。

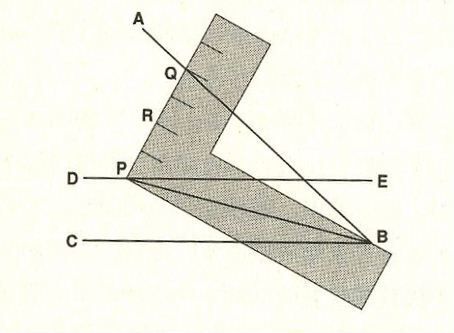
図１）大工の源さんならデキルだよ式の任意の角の３等分。∠ABCを３等分する場合、まず、BCに直角定規の一辺をあて定規の幅でDEを引く（BCとDEは平行）。RはPQの中点で、PRは、定規の一辺の幅に等しい。次に直角定規をPがDE上に、QがAB上にくるように置く。∠ABR=∠RBP=∠PBCとなり、∠ABCを３等分している。

　ところで、このテの直角定規は日本の大工さんも使うわけだが、私らの机の上の三角定規ではダメで、大工さんが使う直角定規ならできるという点に着目したい。たとえば、ニュートンの机の上にも普通の三角定規しかなかったということも十分想像できるわけだ。ニュートンには、スナック芸的な図形パズルの作品もあるというくらいなので、このような問題にチャレンジするチャンスはいくらでもあったはずだが、こと「任意の角を３等分する」という問題に関しては、これといった成果は残していないように思われる（ニュートン作といわれるパズルについてはまた機会を見て触れることにしましょう）。

　とにかく、直角定規のいかにもシンプルな構造に、「理屈を超えた機能の美」というか「道具の美学」というか「プロの仕事」の本当の凄さというものを見てしまうわけです。

「あらよっ」の威力だ

　さて、話は1912年のストックホルムオリンピックに飛ぶ。初めて参加したこのオリンピックの日本選手団は、たったの２人。団長と役員が４人。東京オリンピックの時のカメルーンやコートジボアールの選手団のような雰囲気だったと想像される。団長は、ご存じ講道館の創始者嘉納治五郎。そして、オリンピックの花といわれるマラソンに出場したのが、日本のマラソンの父、当時、東京高師在学中の金栗四三選手だった。世界記録で金メダルも夢ではないという実力に、国民の期待を一身に集めていたのである。当時の富国強兵という政治的バックグラウンドを考えれば、ボルテージの高さがうかがえるというものだろう。

　ところが、この金栗選手と上野浅草の人力車夫が競争をしたところ、あっさり、人力車夫が勝ってしまったという伝説があるらしい。「あらよっ」が、金メダル候補のオリンピック代表を破ってしまったのである！　はたして、ストックホルムオリンピックでの金栗選手はというと、途中棄権、ゴールに姿を現わしたのは、なぜかスタートから３日後というウルトラパフォーマンスとあいなったのだという。

　えっ、何で、こんな話が出てくるのかって？　それは、ホレ、ギリシャの三大難問のひとつ「任意の角を３等分する」という問題が、大工の源さんなら「あらよっ」とばかり解いてしまうというお話で思い出したのだ。同じ「あらよっ」というふうに解釈してもよいでしょう。本当に、その威力というのは恐ろしいほどのものがあるということです。

これちょっとヤバイですよ

　「大工の源さんならデキルだよ」の話、最近出た『The Penguin Dictionary of CURIOUS and INTERESTING Geometry』（David Wells著、Penguin Book刊）という本の中に出てくる。

　この本、タイトルのとおり辞書形式で、２次元、３次元のさまざまな幾何学の話題を紹介していてなかなか楽しい。よく知られた問題もあれば、かなり凝った内容のものも含まれている。ちなみに、「大工の源さんならデキルだよ」（carpenter's-square trisection）の話は、図解入りでこの辞書の１項目となっている。もともと、1928年にアメリカの数学専門誌（『American Mathematical Monthly』）に掲載され衝撃を呼んだものらしい。1928年といえば、この問題の2000年という歴史からすれば、ほんの60数年前のことである。

　たしかに、機械を使えば任意の角の３等分は可能であることは容易に想像できる。しかし、これだけシンプルな道具となると話はちょっと違ってくるというわけだ。その雑誌の記事がどのようなものだったかは知らないが、「先生方、これちょっとヤバイですよ」という雰囲気だったのではないでしょうか。

　ちなみに、「大工の源さんならデキルだよ」とは違うアプローチが『近代プログラマの夕』（拙著、アスキー出版局刊）でも紹介している『Almost Everything There Is to Know』というイギリスの手書き本に１つ出ていたのを思い出した。この本は、かなり古めのこの手のちょっとしたノウハウやアイデアをたくさん紹介しているから、この定規も1928年以前からあったものかもしれない。あるいは、ごく最近作られたものかもしれないが、これも大工さんのアプローチと同じようにあまり知られているわけではない。ただし、大工さんの直角定規がマルチパーパスなのとは違い、こっちは「任意の角を３等分する」ための専用の定規である。大工さんのが普通の包丁ならこっちは回転式リンゴ皮剥き機のようなものである。そうまでして作った定規というのが、図２のような形となっているのである。これを３等分したい角にゴニョゴニョと当ててやる。このゴニョゴニョは相当にズルかもしれないが、とにかく３等分できてしまう。これはこれで、なんというか、いかにも人間のいびつな想像力の産物的で、私は案外好きだったりする。さっとポケットから取り出していきなり見せられたら、何に使うのかまったく意味不明な代物なところがいい。いきなり「任意の角を３等分する」となるのも妙なので、定規のいちばん尖ったところで頭なんか掻いたりなんかして……。いったいどこの先生が、はたまたどういう職業の方が考えられたのでしょうか？

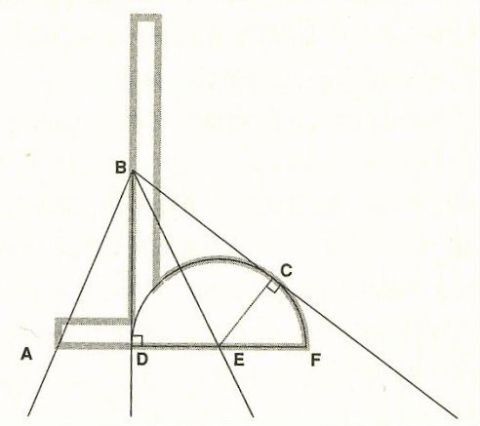
図２）大工の源さんに対抗する任意の角の３等分の方法。かなりキッカイな形をした定規である。AD、DE、EF、ECは、すべて同じ長さである。∠ADBは直角。直角の定規とEを中心にして半径ED（=EC）で描いた円弧からなる。∠ABCを３等分したい場合、縦の直線部分のちょうどよい位置をBに（図では指の先端になっている）、左側の先端をAに、円弧はBCに接するように置く。このとき、∠ABD=∠EBD、∠DBE=∠CBEとなり、∠ABCを３等分している。

　こっちの定規の「理屈コテコテの機能の醜」というか「使い物にならない」というか「いかにも素人の考えオチ」もこれはこれで存在価値があるのかもしれません。

【筆者近況】
遠藤諭（えんどう　さとし）
アスキー総合研究所所長。同研究所の「メディア＆コンテンツサーベイ」の2012年版の販売を開始。その調査結果をもとに書いた「戦後最大のメディアの椅子取りゲームが始まっている」が業界で話題になっている。2012年4月よりTOKYO MXの「チェックタイム」（朝7:00～8:00）で「東京ITニュース」のコメンテータをつとめている。
■関連サイト
・Twitter：@hortense667
・Facebook：遠藤諭